Autómatas finitos

Demostración de la equivalencia entre Autómata Finito determinista (AFD) y Autómata Finito no determinista (AFN) utilizando el método de Construcción de subconjuntos.

Un Autómata Finito determinista (AFD) es una quíntupla $(Q,\Sigma,\delta,s,F)$ donde:

$Q$ es un conjunto finito de estados.
$\Sigma$ es un alfabeto finito.
$\delta : Q \times \Sigma \to Q$ es la función (total) de transición.
$s \in Q$ es el estado inicial.
$F \subseteq Q$ es el conjunto de estados finales (de aceptación).

Un Autómata Finito no determinista (AFN) es una quíntupla $(Q,\Sigma,\delta,s,F)$ donde: ¹

$Q$ es un conjunto finito de estados.
$\Sigma$ es un alfabeto finito.
$\delta : Q \times (\Sigma \cup \{ \veps \}) \to 2^Q$ es la función de transición.
$s \in Q$ es el estado inicial.
$F \subseteq Q$ es el conjunto de estados finales (de aceptación).

Composición de transiciones

La computación en autómatas finitos se puede expresar formalmente como la composición de una secuencia de transiciones. Para esto se generaliza/extiende la definición de función de transición.

Sea $M$ un AFD y $(q, w) \in Q\times\Sigma^\star$. Entonces se define la función $\hat{\delta}$ de transición generalizada que computa el estado resultante de ejecutar $M$ sobre la configuración $(q, w)$ tal que:

$\begin{aligned} \hat{\delta} & : Q \times \Sigma^\star \to Q & \\ \hat{\delta} & (q,\veps) = q & \\ \hat{\delta} & (q, x \cdot v) = \delta(\hat{\delta}(q,v),x) & \end{aligned}$

donde $q \in Q$, $v \in \Sigma^\star$ y $x \in \Sigma$.

Sea $N$ un AFN y $(q,w)\in Q\times\Sigma^\star$. Entonces se define la función $\hat{\delta}$ de transición generalizada que computa el conjunto de los estados resultantes de ejecutar $N$ sobre la configuración $(q, w)$ tal que:

$\begin{aligned} \hat{\delta} & : Q \times \Sigma^\star \to 2^Q & \\ \hat{\delta} & (q,\veps) = C_\veps(q) & \\ \hat{\delta} & (q, x \cdot v) = C_\veps \left( \bigcup\limits_{r \;\in\; \hat{\delta}(q,v) }^{} \delta(r,x) \right) & \end{aligned}$

donde:

$q \in Q$, $v \in \Sigma^\star$ y $x \in \Sigma$.
$C_\veps(q)$ es la clausura respecto de $\veps$ para el estado $q$, esto es el conjunto de todos los estados alcanzables desde $q$ usando únicamente transiciones $\veps$.
Sea $Q$ un conjunto de estados, $C_\veps(Q) = \bigcup\limits_{q \; \in \; Q}^{} C_\veps(q)$

Aceptación

El lenguaje aceptado (o reconocido) por un autómata se puede expresar en términos de $\hat{\delta}$.

Sea $M=(Q,\Sigma,\delta,s,F)$ un AFD. Entonces el lenguaje $\mathcal{L}(M)\subseteq\Sigma^\star$ aceptado por $M$ se define:

$\mathcal{L}(M)=\{ w \in \Sigma^\star \ \mid \ \hat{\delta}(s,w) \in F \}$

Sea $N=(Q,\Sigma,\delta,s,F)$ un AFN. Entonces el lenguaje $\mathcal{L}(N)\subseteq\Sigma^\star$ aceptado por $N$ se define:

$\mathcal{L}(N)=\{ w \in \Sigma^\star \ \mid \ \hat{\delta}(s,w) \cap F \neq \varnothing \}$

Árbol de cómputo

La computación en autómatas finitos se puede ilustrar gráficamente en forma de árbol.

La computación no determinista es un árbol de cómputo donde:

La raíz corresponde al inicio de la computación.
Cada punto de ramificación corresponde a un punto de la computación en la cual la máquina tiene múltiples opciones.
La máquina acepta la entrada si al menos una de las ramas de cómputo termina en un estado de aceptación. En caso contrario, rechaza.
Las ramas de cómputo que aceptan o rechazan son del mismo largo.
Si en un punto de ramificación no hay una opción de transición para el estado actual y símbolo actual de la entrada entonces la máquina queda atorada.

En contraste, la computación determinista es lineal representándose con una sola rama, y nunca queda atorada, es decir siempre acepta o rechaza. ²

Es fácil notar que cualquier computación determinista se puede ver como una computación no determinista donde hay solo una rama de cómputo, pero no es tan fácil notar el recíproco.

Equivalencia AFD-AFN

Sean $M$ y $M’$ autómatas. Entonces $M$ y $M’$ son equivalentes, denotado $M=M’$, si y solo si $M$ y $M’$ aceptan el mismo lenguaje. Es decir:

$M = M' \ \iff \ \mathcal{L}(M) = \mathcal{L}(M')$

AFD simulado por AFN

Para todo AFD $D$ existe un AFN $N$ tal que $D = N$.

Podemos ver al AFD como un caso especial de AFN sin transiciones $\veps$ donde para todo par $(q,x) \in Q\times\Sigma$ se cumple $\len{\delta(q, x)} = 1$.

Por lo tanto, cualquier lenguaje aceptado por un AFD puede ser aceptado por un AFN.

AFN simulado por AFD

Presentamos el método de Construcción de subconjuntos para construir un AFD a partir de un AFN.

Intuición

Para cualquier AFN, necesitamos poder construir un AFD que pueda simular el funcionamiento del AFN. Para simular el AFN, en cada paso de la computación el AFD necesita recordar los posibles conjuntos de estados en los que puede estar el AFN. Si el AFN tiene $k$ estados, hay $2^k$ subconjuntos de estados posibles que el AFD tiene que recordar, por lo cual el AFD tendrá $2^k$ estados.

En la práctica, no todos los $2^k$ estados resultantes serán alcanzables. Los estados no alcanzables pueden ser ignorados o eliminados sin afectar la equivalencia con el AFN ya que el lenguaje reconocido será el mismo.

Considerar el AFN $M=(\{ q_1, q_2, q_3, q_4\}, \{\texttt{a},\texttt{b}\},\delta,q_1,\{ q_4 \})$ , representado por el siguiente diagrama de transiciones:

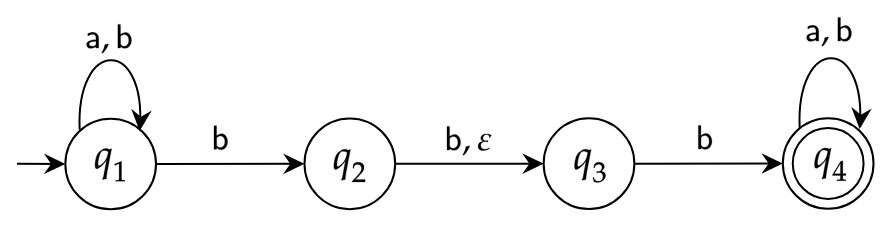
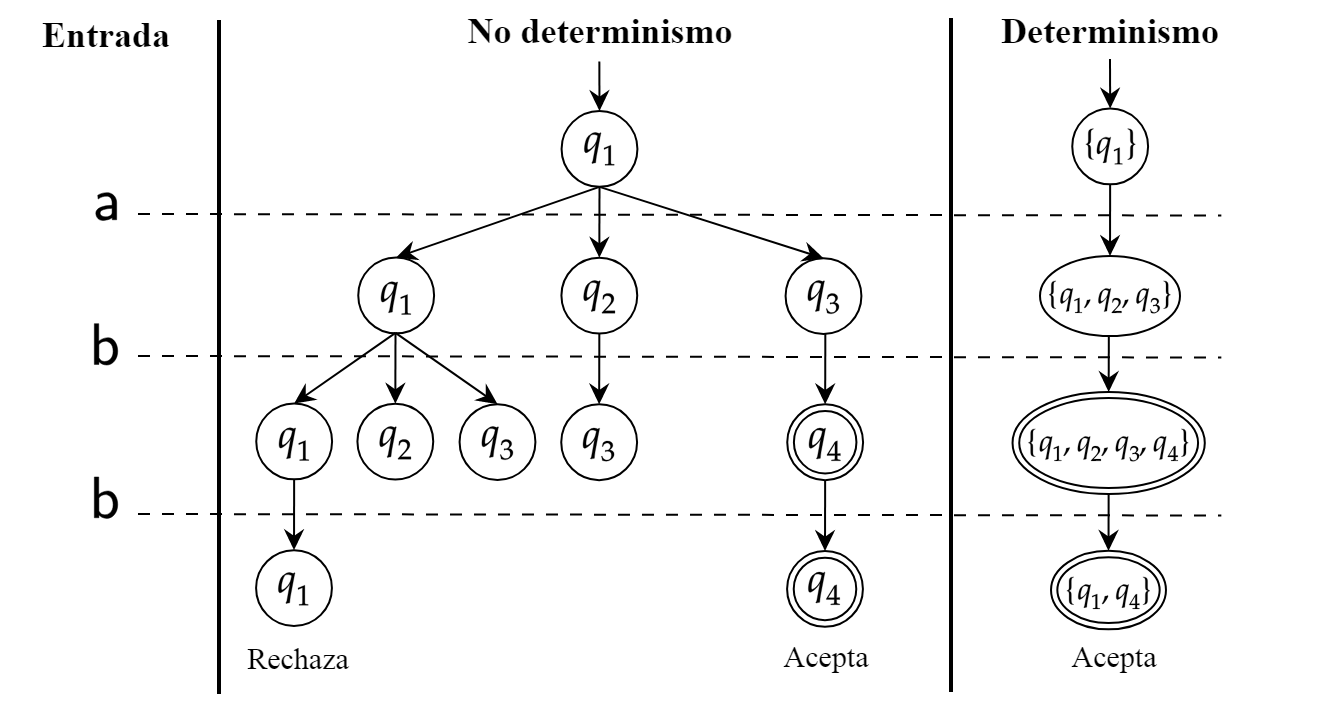
La computación de $M$ sobre la entrada $w=\texttt{a}\,\texttt{b}\,\texttt{b}$ resulta en una rama que acepta, por lo tanto $w \in L(M)$. A continuación ilustramos este resultado junto a la versión determinista correspondiente:

Formalización

Sea $N=(Q,\Sigma,\delta,s,F)$ un AFN. Entonces $SC(N)=(Q^\prime,\Sigma,\delta^\prime,s^\prime,F^\prime)$ es el AFD resultante de aplicar sobre $N$ el método de construcción de subconjuntos tal que:

$Q^\prime = 2^Q$
Los estados de $SC(N)$ son los posibles sub-conjuntos de estados de $N$, esto es $\mathcal P \left({Q}\right)$.
$\delta^\prime(R, x) = C_\veps \left( \bigcup\limits_{r \;\in\; R}^{} \delta(r, x) \right)$
Para $R \in Q^\prime$ y $x \in \Sigma$, la transición en $SC(N)$ es la unión de los estados alcanzables leyendo $x$ para cada $r \in R$ según $\delta$, junto a los estados alcanzables a través de transiciones $\veps$.
$s^\prime = C_\veps( \{ s \} )$
El autómata $SC(N)$ comienza en el conjunto de estados alcanzables a través de transiciones $\veps$ desde $s$.
$F^\prime = \{ R \in Q^\prime \ \mid \ R \cap F \neq \varnothing \}$
El autómata $SC(N)$ acepta la entrada si termina en un estado que contiene al menos un estado final del autómata $N$.

Observaciones:

El alfabeto $\Sigma$ permanece sin cambios.
En el caso de un AFN sin transiciones $\veps$, podemos omitir el uso de $C_\veps$ en los pasos 2 y 3.

Sea $N=(Q,\Sigma,\delta,s,F)$ un AFN y $SC(N)=(Q^\prime,\Sigma,\delta^\prime,s^\prime,F^\prime)$ un AFD. Entonces:

$\forall\,w\in\Sigma^\star \,:\, \hat{\delta^\prime}(s^\prime, w) = \hat{\delta}(s, w)$

Por inducción estructural en $w \in \Sigma^\star$: ³

Caso Base. Sea $w=\veps$.

$\begin{aligned} \hat{\delta^\prime}(s^\prime, w) &= \hat{\delta^\prime}(s^\prime, \veps) && \\ &= s^\prime && \text{(def. 3)} \\ &= C_\veps( \{ s \} ) && \text{(def. 8)} \\ &= \hat{\delta}(s, \veps) && \text{(def. 4)} \\ &= \hat{\delta}(s, w) && \end{aligned}$

Paso Inductivo. Sea $w=x \cdot v$ con $x \in \Sigma$, $v \in \Sigma^\star$ y $|v| \geq 0$:
HI. $\hat{\delta^\prime}(s^\prime, v) = \hat{\delta}(s, v)$
T. $\hat{\delta^\prime}(s^\prime, x \cdot v) = \hat{\delta}(s, x \cdot v)$

$\begin{aligned} \hat{\delta^\prime}(s^\prime, w) &= \hat{\delta^\prime}(s^\prime, x \cdot v) && \\ &= \delta^\prime(\hat{\delta^\prime}(s^\prime, v), x) && \\ &= \delta^\prime(\hat{\delta}(s, v), x) && \text{(por HI)} \\ &= C_\veps \left( \bigcup\limits_{r \;\in\; \hat{\delta}(s, v)}^{} \delta(r, x) \right) && \\ &= \hat{\delta}(s, x \cdot v) && \\ &= \hat{\delta}(s, w) && \end{aligned}$

Sea $N=(Q,\Sigma,\delta,s,F)$ un AFN y $SC(N)=(Q^\prime,\Sigma,\delta^\prime,s^\prime,F^\prime)$ un AFD. Entonces $\mathcal{L}(N)=\mathcal{L}(SC(N))$. $\label{lema3}$

Para $w\in\Sigma^\prime$ arbitrario:

$\begin{aligned} w\in\mathcal{L}(N) &\,\iff\, \hat{\delta}(s,w) \cap F \neq \varnothing && \text{(def. 6)} \\ &\,\iff\, \hat{\delta^\prime}(s^\prime,w) \cap F \neq \varnothing && \text{(lema 2)} \\ &\,\iff\, \hat{\delta^\prime}(s^\prime,w) \in F^\prime && \text{(def. 8)} \\ &\,\iff\, w\in\mathcal{L}(SC(N)) && \text{(def. 5)} \end{aligned}$

Por lo tanto $\mathcal{L}(N)=\mathcal{L}(SC(N))$.

Equivalencia

Sea $L\subseteq\Sigma^\star$. Entonces existe un AFD $D$ tal que $\mathcal{L}(D)=L$ si y solo si existe un AFN $N$ tal que $\mathcal{L}(N)=L$.

Procedemos en ambas direcciones:

Solo Si: Sea $D$ un AFD tal que $\mathcal{L}(D)=L$. Por el lema 1 hay un AFN $N$ tal que $D=N$, o sea que se cumple $\mathcal{L}(D)=\mathcal{L}(N)$, entonces $\mathcal{L}(N)=L$.
Si: Sea $N$ un AFN tal que $\mathcal{L}(N)=L$. Aplicando el método de la definición 8 obtenemos un AFD $D=SC(N)$ que simula el funcionamiento de $N$. Por el lema 3 se cumple $\mathcal{L}(N)=\mathcal{L}(D)$, entonces $\mathcal{L}(D)=L$.

Como consecuencia del Teorema 1, AFD y AFN tienen el mismo poder expresivo (o poder de cómputo) ya que ambos son capaces de aceptar la misma clase de lenguajes.

Referencias

Se puede considerar un tipo especial de AFN que no admite transiciones $\veps$. En este caso la función de transición se define como $\delta : Q\times\Sigma \to 2^Q$. ↩
De ser conveniente, se le puede permitir al AFD quedar atorado al no haber transición disponible para un estado y símbolo. Esto significa que la función de transición es parcial. Sin embargo, esta no es la concepción mas común de AFD. ↩
Alternativamente se puede hacer una inducción sobre el largo de la cadena $w$. Esto es, en el CB $\len{w}=0$, en el PI asumimos para $\len{w}=k$ con $k \geq 0$ y luego demostramos para $\len{w}=k+1$. ↩

Bibliografía

Sipser, M. (2012). Introduction to the Theory of Computation (2nd ed.). Course Technology.
J. Hopcroft, R. M. & J. U. (2000). Introduction to Automata Theory, Languages, and Computation (2nd ed.). Addison Wesley.