Base del logaritmo en notación Big O

En el análisis de algoritmos es conveniente a veces omitir la base del logaritmo al tratar con costos logarítmicos asintóticos expresados en la notación $O(\_)$ . Por ejemplo, si la búsqueda binaria tiene en el peor caso un costo de $\lfloor\log_2 x + 1\rfloor$ comparaciones, entonces decimos que este costo es de orden $O(\log_2 x)$ o simplemente $O(\log x)$, aunque se pierda información. Este es un “abuso de notación” válido.

Intuición

Los logaritmos en diferentes bases difieren únicamente en un factor constante, estos factores son despreciados en la notación $O(\_)$ y sus semejantes $\Theta(\_)$ y $\Omega(\_)$ . Por lo tanto, todos los logaritmos pertenecen al mismo orden de crecimiento.

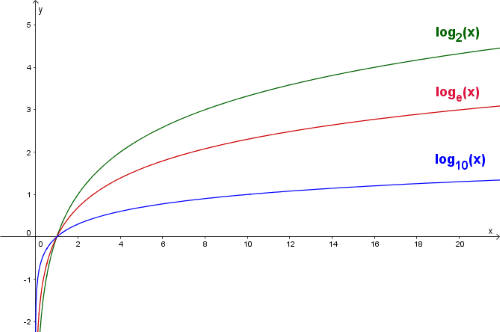
Algo similar sucede con las funciones de la forma $\log_\alpha (x^c)$. Por propiedad de logaritmos:

$\log_\alpha (x^c) = c \log_\alpha x$

entonces

$O(\log_\alpha (x^c)) = O(c \log_\alpha x) = O(\log x)$

Definiciones

Sean las funciones $f,g \ \colon \mathbb{R}\to\mathbb{R}$. Entonces $f$ es $O(g)$ si y solo si existen constantes $c \gt 0$ y $x_0$ tal que para todo $x \geq x_0$ : $\len{f(x)} \leq c \cdot \len{g(x)}$. Es decir:

$f \in O(g) \ \iff \ \exists\,c \gt 0 \,:\, \exists\,x_0 \,:\, \forall\,x \geq x_0 \,:\, \len{f(x)} \leq c \cdot \len{g(x)}$

Sean las funciones $f,g\ \colon \mathbb{R}\to\mathbb{R}$. Entonces $f$ es $O(g)$ si y solo si $f$ esta acotado superiormente por $g$ cuando $x \to \infty$ (asumiendo $g(x) \neq 0$). Es decir:

$f \in O(g) \ \iff \ \limsup_{x \to \infty} \len{\frac{f(x)}{g(x)}} = c \quad \text{con } c \in \lbrack 0,\infty)$

Resultados útiles

Sea $\log_{\alpha} x$ el logaritmo en base $\alpha$ de $x$. Entonces:

$\log_{\alpha} x = \frac{\log_{\beta} x}{\log_{\beta} \alpha}$

Sean $z$ e $y$ funciones tal que:

$\begin{aligned} y &= \log_{\alpha} x \iff \alpha^y = \alpha^{\log_{\alpha} x} = x \\ z &= \log_{\beta} x \iff \beta^z = \beta^{\log_{\beta} x } = x \end{aligned}$

Luego:

$\begin{aligned} z &= \log_{\beta} x \\ &= \log_{\beta} (\alpha^y) \\ &= y \cdot \log_{\beta} \alpha \\ &= \log_{\alpha} x \cdot \log_{\beta} \alpha \end{aligned}$

Por lo tanto, si

$\log_{\beta} x = \log_{\beta} \alpha \cdot \log_{\alpha} x$

entonces

$\log_{\alpha} x = \frac{\log_{\beta} x}{\log_{\beta} \alpha}$

donde $\log_{\beta} \alpha$ es un factor constante.

Sea $\log_{\alpha} x$ el logaritmo en base $\alpha$ de $x$. Entonces:

$\frac{d}{dx}(\log_{\alpha} x) = \frac{1}{x \log_{e} \alpha}$

Comenzamos con el caso particular $\alpha=e$:

$\begin{aligned} y &= \log_{e} x & \\ e^y &= e^{\log_{e} x} & \\ &= x & \end{aligned}$

Diferenciando respecto a $x$ en ambos lados: ¹

$\begin{aligned} \frac{d}{dx} e^y &\ = \ \frac{d}{dx} x & \\ \frac{d}{dy} e^y \cdot \frac{d}{dx} y &\ = \ 1 & \text{regla de la cadena} \\ e^y \cdot \frac{d}{dx} y &\ = \ 1 & \\ \frac{d}{dx} y &\ = \ \frac{1}{e^y} & \\ \frac{d}{dx} (\log_{e} x) &\ = \ \frac{1}{e^{\log_{e} x}} & \\ &\ = \ \frac{1}{x} & \end{aligned}$

Luego, para el caso general usamos el resultado previo y el Lema 1:

$\begin{aligned} \frac{d}{dx}(\log_{\alpha} x) &= \frac{d}{dx} \left(\frac{\log_{e} x}{\log_{e} \alpha}\right) & \text{Lema 1 con } \beta=e \\ &= \frac{1}{\log_{e} \alpha} \cdot \frac{d}{dx} \left(\log_{e} x \right) & \\ &= \frac{1}{\log_{e} \alpha} \cdot \frac{1}{x} & \text{resultado anterior} \\ &= \frac{1}{x \log_{e} \alpha} & \end{aligned}$

Sean $f$ y $g$ dos funciones continuas definidas en el intervalo $[a,b]$ y derivables en $(a,b)$ con $c \in (a,b)$ tal que:

$\lim_{x \to c} f(x) = \lim_{x \to c} g(x) = 0$ o $\pm\infty$
Para todo $x \in (a,b)$: $g’(x) \neq 0$
Existe $\lim_{x \to c} \frac{f’(x)}{g’(x)} = L$ con $L \in \mathbb{R}$

Entonces:

$\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)} = L$

Teorema principal

Sean $\alpha,\beta \in \mathbb{R}$ tal que $\alpha \gt 1$ y $\beta \gt 1$. Entonces: $\ \log_{\alpha} x$ es $O(\log_{\beta} x)$

Demostración 1

Por la definición 1.1:

$\log_{\alpha} x \in O(\log_{\beta} x) \iff \exists\,c\gt 0 \,:\, \exists\,x_0 \,:\, \forall\,x \geq x_0 \,:\, \len{\log_{\alpha} x} \leq c \cdot \len{\log_{\beta} x}$

Por el lema 1 tenemos:

$\log_{\alpha} x \leq \frac{\log_{\beta} x}{\log_{\beta} \alpha}$

La función $\log$ es negativa en $(0,1)$. Tomamos valor absoluto:

$\begin{aligned} \len{\log_{\alpha} x} &\leq \len{ \frac{\log_{\beta} x}{\log_{\beta} \alpha} } & \\ &= \len{ \frac{1}{\log_{\beta} \alpha} \cdot \log_{\beta} x } & \\ &= \frac{1}{\log_{\beta} \alpha} \cdot \len{ \log_{\beta} x } & \end{aligned}$

Donde $c = \frac{1}{\log_{\beta} \alpha} \gt 0$, y podemos seleccionar cualquier $x_0 \gt 0$.

Por lo tanto $\log_{\alpha} x \in O(\log_{\beta} x)$.

Demostración 2

Por la definición 1.2:

$\log_{\alpha} x \in O(\log_{\beta} x) \iff \limsup_{x \to \infty} \len{\frac{\log_{\alpha} x}{\log_{\beta} x}} = c \quad \text{con } c \in \lbrack 0,\infty)$

La función $\log$ es continua, derivable y estrictamente creciente en todo su dominio, por esto el límite siempre existe y prescindimos del supremo. Además, $\log$ es positiva en $(1, \infty)$ y por esto también prescindimos del valor absoluto. Luego:

$\lim_{x \to \infty} \frac{\log_{\alpha} x}{\log_{\beta} x} = \frac{\infty}{\infty}$

Para levantar la indeterminación $\frac{\infty}{\infty}$ aplicamos el lema 3:

$\begin{aligned} \lim_{x \to \infty} \frac{\log_{\alpha} x}{\log_{\beta} x} &= \lim_{x \to \infty} \frac{\log_\alpha^\prime x}{\log_\beta^\prime x} & \text{Lema 3} \\ &= \lim_{x \to \infty} \frac{\frac{1}{x \log_e \alpha}}{\frac{1}{x \log_e \beta}} & \text{Lema 2} \\ &= \lim_{x \to \infty} \frac{\log_e \beta}{\log_e \alpha} & \\ &= \frac{\log_e \beta}{\log_e \alpha} & \end{aligned}$

Donde $c = \frac{\log_e \beta}{\log_e \alpha} \in \lbrack 0,\infty)$. ²

En particular, si $\beta = e$, entonces: $c=\frac{\log_e e}{\log_e \alpha}=\frac{1}{\log_e \alpha} \gt 0$.

Por lo tanto $\log_{\alpha} x \in O(\log_{\beta} x)$.

Como consecuencia del Teorema 1, se acostumbra omitir la base $\beta$ escribiendo simplemente $\log_{\alpha} x \in O(\log x)$. Esto se puede demostrar similarmente para $\Theta(\_)$ y $\Omega(\_)$ .

Referencias

Aquí se asume $\log x$ diferenciable. Una alternativa sin este requerimiento es aplicar el Teorema de la Función Inversa. ↩
Siendo más preciso, $\frac{\log_e \beta}{\log_e \alpha} \in (0,\infty)$ porque nunca puede ser 0. Este resultado satisface la definición por límite de $\Theta(\_)$ , por lo tanto se tiene un resultado más fuerte: $\log_{\alpha} x \in \Theta(\log_{\beta} x)$, lo cual implica $\log_{\alpha} x \in O(\log_{\beta} x)$ y $\log_{\alpha} x \in \Omega(\log_{\beta} x)$. ↩