Demostración asistida por máquina de un teorema de Teoría de Números: Todo número natural compuesto $n$ tiene un divisor primo $p$ menor o igual que $\sqrt{n}$. El teorema se formaliza parcialmente en un sistema de Deducción Natural y se expresa mediante el lenguaje Isar en el asistente interactivo Isabelle.
Teoría
Sean $a, b \in \mathbb{N}$ y $a \neq 0$. Entonces $a$ divide $b$, denotado por $a \mid b$, si existe $c \in \mathbb{N}$ tal que $b = a\ c$. Cuando $a \mid b$ decimos que $a$ es divisor de $b$ y que $b$ es múltiplo de $a$.
Un número natural $n$ mayor a 1 es primo si y solo si los únicos divisores que posee son 1 y $n$.
Un número natural $n$ mayor a 1 es compuesto si y solo si no es primo, es decir que posee más de dos divisores.
A partir de las dos definiciones precedentes se sigue que $0$ y $1$ no son números primos ni compuestos. Observaciones:
- El $0$ es divisible por todo número natural, es decir $n \cdot 0 = 0$. También podríamos decir
que no es divisible en absoluto si decidimos excluirlo de los números naturales.
Por otro lado, este mismo argumento no sirve para justificar la no primalidad de $1$. -
Por el Teorema Fundamental de la Aritmética, todo número natural tiene una representación única de factores primos. Pero sucede que el $0$ solopuede representarse a si mismo y no es una representación única:
Por otro lado, si $1$ fuera primo, podríamos tener que:
Por lo tanto, ni $0$ ni $1$ sirven a los propósitos del TFA.
Todo número natural $n$ mayor a 1 es mayor o igual a sus divisores.
Supongamos $n>0$ y $d\mid n$. Luego por definición de divisor $\exists\ q \in\mathbb{N}$ tal que $n=d\,q$. Además $d \leq d\ q$. Por lo tanto $d \leq n$.
Este resultado puede generalizarse para .
Todo número natural mayor a 1 tiene al menos un divisor primo.
Por el Teorema Fundamental de la Aritmética (TFA), todo número natural mayor a 1 se puede factorizar como un conjunto único de números primos. Por lo tanto, todo número natural mayor a 1 tiene al menos un divisor primo.
Otras demostraciones de este lema también son posibles sin apelar al TFA.
Todo número natural compuesto $n$ se puede expresar como el producto de dos naturales, $a$ y $b$, estrictamente mayores a 1 y menores a $n$. Además $a$ y $b$ no son necesariamente distintos.
Sea $n$ un número compuesto. Entonces $\exists\ a\in\mathbb{N}$ tal que $a \mid n$ con $a\not = 1$ y $a\not = n$. Si $a \mid n$, por definición de divisor: $\exists\ b\in\mathbb{N}$ tal que $n=a\ b$.
Por Lema 1, si $a \mid n$ entonces $a \leq n$. Pero $a \not = n$, entonces $a \lt n$. Además como $1 \mid a$, entonces $1 \leq a$. Pero $a \not = 1$, entonces $1 \lt a$. Hasta aquí tenemos que: $1 \lt a \land a \lt n$.
Como $a \not = n$ y $n = a\ b$, entonces $b \not = 1$. De manera similar, como $a \not = 1$ entonces $b \not = n$. Así que tenemos: $b \mid n$ con $b \not = 1 \land b \not = n$. Finalmente, si razonamos como en el párrafo anterior para $a$, se concluye además que: $1 \lt b \land b \lt n$.
Todo número natural compuesto $n$ tiene un divisor primo $p$ menor o igual que $\sqrt{n}$.
Sea $n$ un número compuesto. Por lema 3 podemos expresar $n$ como $n = a\ b$ donde $a,b \in \mathbb{N}$ con $1 \lt a \lt n$ y $1 \lt b \lt n$.
Primero veamos que necesariamente $a \leq \sqrt{n} \lor b \leq \sqrt{n}$. Para esto supongamos por el contrario que $\sqrt{n} \lt a \land \sqrt{n} \lt b$, entonces tenemos que:
Pero esto es absurdo, por lo tanto: $a \leq \sqrt{n} \lor b \leq \sqrt{n}$.
Ahora procedemos por casos:
- Si $a \leq \sqrt{n}$: sabemos por Lema 2 que hay un $p \in \mathbb{P}$ tal que $p \mid a$. Además por lema 1 $p \leq a$, y por lo tanto $p \leq a \leq \sqrt{n}$. Por otro lado, como $n=a\ b$, entonces $a \mid n$. La relación de división en $\mathbb{N}$ es un orden parcial, por lo tanto si $p \leq a$, también vale $p \mid n$.
- Si $b \leq \sqrt{n}$: razonamiento análago al caso I.
Finalmente, para ambos casos se sigue que $(\exists p)(p\in\mathbb{P} \land p \mid n \land p \leq \sqrt{n})$.
Aplicaciones
El Teorema 1 es particularmente útil en el problema de determinar la primalidad de un número dado $n$. En el enfoque ingenuo, si probamos dividir $n$ entre $2, 3, 4, 5, … , n-1$ y alguna de estas divisiones es exacta, es decir da resto cero, podemos asegurar que el número $n$ es compuesto. Si ninguna de las divisiones es exacta, $n$ es primo.
Pero podemos hacer este procedimiento más eficiente, el teorema nos dice que si un número es compuesto alguno de sus factores (excepto el 1) debe ser menor o igual que $\sqrt{n}$, y esto significa que basta con probar dividir $n$ entre $2, 3, 4, 5, … , \sqrt{n}$, pues de tener un divisor mayor que $\sqrt{n}$ tendría otro más pequeño que ya habríamos comprobado.
Para probar que 227 es primo, sabiendo que $\sqrt{227} = 15,06…$ basta con probar que 227 no es divisible entre 2, 3, 5, 7, 11 y 13.
El método de la Criba de Eratóstenes permite obtener todos los números primos menores o iguales que un número dado. Por el teorema 1, no es necesario recorrer todo el intervalo $[2,n]$, basta con recorrer hasta $\lfloor\sqrt{n}\rfloor$. No obstante, este refinamiento no modifica el comportamiento asintótico temporal del algoritmo.
\begin{algorithm}\begin{algorithmic}
\PROCEDURE{sieve}{$n$}
\FOR{$k := 1$ \TO $n$}
\STATE \uppercase{S}$[k] :=$ \TRUE
\ENDFOR
\STATE \uppercase{S}$[1] :=$ \FALSE
\FOR{$p := 2$ \TO $\lfloor\sqrt{n}\rfloor$}
\IF{\uppercase{S}$[p] \neq $ \FALSE}
\FOR{$k := p$ \TO $\lfloor\frac{n}{p}\rfloor$}
\STATE \uppercase{S}$[k \times p] :=$ \FALSE
\ENDFOR
\ENDIF
\ENDFOR
\ENDPROCEDURE
\end{algorithmic}\end{algorithm}
Formalización en Deducción Natural
Formalizamos la estructura general de la demostración del teorema 1 en un sistema de Deducción Natural. A continuación lo presentamos en dos estilos. 1
Estilo Gentzen

Sub-árbol B:
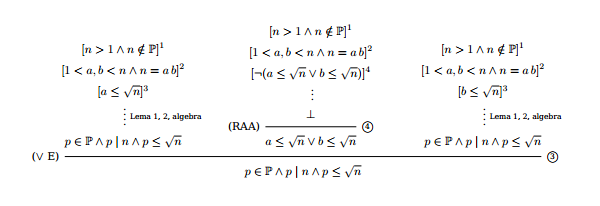
Estilo Fitch

Formalización en Isabelle/Isar
Estructura general de la demostración del teorema 1 en Isar.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
lemma Lema_1: "∀ n d::nat.(n>0 ∧ d dvd n ⟶ d ≤ n)"
sorry
lemma Lema_2: "∀ n::nat.(n>1 ⟶ (∃p. (prime p) ∧ (p dvd n)))"
sorry
lemma Lema_3: "∀ n::nat.(n>1 ∧ ¬(prime n) ⟶ (∃a b::nat. 1<a ∧ a<n ∧ 1<b ∧ b<n ∧ n=a*b))"
sorry
theorem Teorema_1: "∀ n::nat.(n>1 ∧ ¬(prime n) ⟶ (∃ p::nat.(prime p) ∧ (p dvd n) ∧ p ≤ sqrt n))"
proof
fix n
show "n>1 ∧ ¬(prime n) ⟶ (∃ p.(prime p) ∧ (p dvd n) ∧ p ≤ sqrt n)"
proofj
assume H1: "n>1 ∧ ¬(prime n)"
show "∃ p. (prime p) ∧ (p dvd n) ∧ (p ≤ sqrt n)"
proof -
from Lema_3
have "(n>1 ∧ ¬(prime n) ⟶ (∃ a b::nat.1<a ∧ a<n ∧ 1<b ∧ b<n ∧ n=a*b))"
by(rule allE)
from this and H1
have "∃ a b::nat. 1<a ∧ a<n ∧ 1<b ∧ b<n ∧ n=a*b"
by (rule mp)
from this obtain a
where "∃ b::nat. 1<a ∧ a<n ∧ 1<b ∧ b<n ∧ n=a*b"
by (rule exE)
from this obtain b
where H2: "1<a ∧ a<n ∧ 1<b ∧ b<n ∧ n=a*b"
by (rule exE)
have "a ≤ sqrt n ∨ b ≤ sqrt n"
proof (rule ccontr)
assume H4: "¬ (a ≤ sqrt n ∨ b ≤ sqrt n)"
(* ... *)
show False by(rule notE)
qed
then show "∃ p.((prime p) ∧ (p dvd n) ∧ (p ≤ sqrt n))"
proof
assume H3: "a ≤ sqrt n"
(* ... Lemas 1 y 2, algebra ... *)
show "∃ p.((prime p) ∧ (p dvd n) ∧ (p ≤ sqrt n))" by (rule exI)
next
assume H3: "b ≤ sqrt n"
(* ... Lemas 1 y 2, algebra ... *)
show "∃ p.((prime p) ∧ (p dvd n) ∧ (p ≤ sqrt n))" by (rule exI)
qed
qed
qed
Referencias
-
La regla $(\exists\ \text{E}) \times 2$ es un abuso de notación que denota dos aplicaciones sucesivas de la regla de eliminación del existencial. ↩
Bibliografía
- Cohn, P. M. (1982). Algebra - Volume 1 (2nd ed.). Wiley.
- Wenzel, M. (2016). The Isabelle/Isar Reference Manual.